Euclidean Vectors in Flash

Euclidean vectors are objects in geometry with certain properties that are very useful for developing games. They can be seen as points, but they also have a magnitude and a direction. They are represented as arrows going from the initial point to the final point, and that’s how we will draw them in this article.

Euclidean vectors are commonly used in mathematics and physics for a lot of things: they can represent velocity, acceleration and forces in physics, or help prove a lot of important theorems in mathematics. In this tutorial, you’ll learn about Euclidean vectors, and build a class that you can use in your own Flash projects.

Please note that Euclidean vectors are different than ActionScript’s Vector class, and also different than vector drawing.

Vectors can be used in the Flash environment to help you achieve complex tasks that would otherwise require a lot of effort if done without them. In this article you will learn how to use them in Flash, as well as learn a lot of cool tricks with vectors.

---

Step 1: Cartesian Coordinates and Flash’s Coordinates

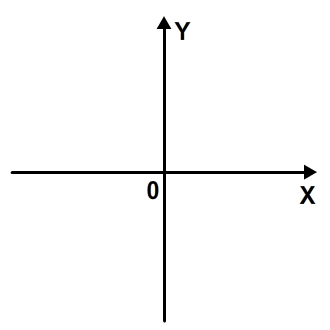
Before jumping into vectors, let’s introduce Flash’s coordinate system. You are probably familiar with the Cartesian coordinate system (even if you don’t know it by name):

Flash’s system is very similar. The only difference is that the y-axis is upside-down:

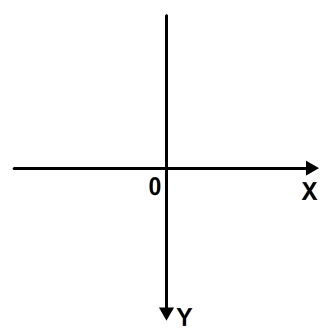
When we start working with vectors in flash, we need to remember that. However, good news: this different system doesn’t make much difference. Working with vectors in it will be basically like working with vectors in the Cartesian system.

---

Step 2: Defining a Vector

For the purpose of this tutorial, we will define and work with all vectors’ initial points as being the registration point of the stage, just as they are commonly used in mathematics. A vector will then be defined just like a common point, but it will have magnitude and angle properties. Take a look at some example vectors defined in the stage:

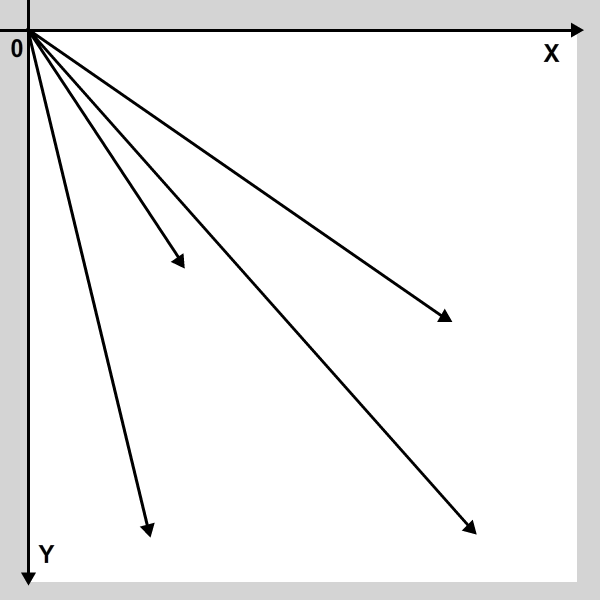
As you can see, a vector is represented by an arrow, and each vector has a certain length (or magnitude) and points along a certain angle. The tail of each vector is at the registration point (0, 0).

We will create a simple EuclideanVector class for this tutorial, using the Point class to hold the vector’s coordinates. Let’s create the basic vector class now:

package
{
 import flash.geom.Point;

 public class EuclideanVector
 {
  public var position:Point;
  public var magnitude:Number;
  public var angle:Number;

  public function EuclideanVector(endPoint:Point)
  {
   position = endPoint;
  }
 }
}

During this tutorial, we will talk about the sense and the direction of a vector. Note that the direction just defines a line that “contains” the vector. The sense is what defines which way the vector points along this line.

---

Step 3: Inverse of a Vector

In this tutorial we will use the expression “inverse of a vector”. The inverse of a vector is another vector with the same magnitude and direction, but a contrary sense. That translates to a vector with the opposite signal of the first vector’s coordinates. So a vector with an endpoint of (x, y) would have an inverse vector with an endpoint of (-x, -y).

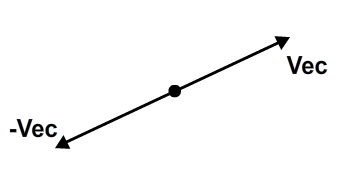
Let’s add a function to our EuclideanVector class to return the inverse vector:

public function inverse():EuclideanVector
{
 return new EuclideanVector(new Point(-position.x, -position.y));
}

---

Step 4: Basic Operations Addition

Read more: Euclidean Vectors in Flash